Now we’ll take a more technical look at our initial granular synthesis development in Unity3D. In this post, we’ll cover human hearing thresholds, granular synth basics, and how to overcome some of the challenges when performing DSP against the unstable timing of game engine frame rates.
Audio Processing and Perception
Just to cement how important audio timing is in any sound-focused platform, let me briefly talk about thresholds in auditory perception. Humans have a highly developed ability for noticing minor fluctuations of sound. For instance, a 4 ms disruption (silence) within an otherwise continuous 600 Hz sine wave appears as a noticeable pop (Roads, 2001). This threshold moves to 20 ms in harmonically rich sound, such as pink noise. A similar sensitivity is demonstrated in pitch variations, where subjects were shown to detect a difference between a tone of 1000 Hz against a 996.5 Hz tone (Lorenzi & Chaix, 2019).
TLDR: Our ears are extremely sensitive to aliasing and timing issues, and so we need to keep this in mind when we build our DSP chain and synthesisers.
Our ears are extremely sensitive to aliasing and timing issues, and so we need to keep this in mind when we build our DSP chain and synthesisers.
When programming for games and other interactive experiences that aren’t focused on music creation, the issue of sonic timing is of less concern. That’s not to say that a satisfyingly realistic audio/visual event in a game of, say, a gun firing, doesn’t need tight synchronisation between the visual animation and the audio clip. But, it is perfectly reasonable to except that audio event only needs to occur during the visual frame update, since that’s when the action happens. Audio-focused software, on the other hand, needs to trigger and manipulate data as close to the sample rate (often 44,100 Hz) as possible. This is because a user’s experience is bound to their sensitive perception of sound.
Acknowledgement
Let me acknowledge that our granular synthesiser development began by picking apart Manual Eisl’s “Granulator” code from GitHub. While it’s a very simple example, it demonstrated a very fitting approach to leveraging OnAudioFilterRead granular synthesis. It’s well worth a look if you’d like to start building your own synthesis implementation in Unity3D.
Basic Synthesis Design in Unity3D
The basic programmatic flow that underpins our granular synthesiser is as follows:
- A grain manager stores the samples of an audio clip in an array.
- Each update call (frame), the manager determines how many grains it should queue for the next frame based on the rate at which the user has set (generally between 1ms and 200ms). Note: that typically this is called rate or derived as a parameter called density, however we call this cadence to avoid confusion between other parameters in our environment.
- Each grain is provided an array filled with concurrent audio samples from the clip, starting at the grain’s playhead position, and with a length that equals it’s duration (generally between 20ms and 200ms, but can be longer).
- The grain array is then shaped using a windowing function to quickly fade the sound in and out, avoiding clicks and pops that would occur without it.
- Any DSP effects (filtering, chorus, distortion, etc) is then applied to the grain array.
- The final grain audio buffer is written into the audio source’s OnAudioFilterRead buffer, which is spatialised by Unity3D and combined together with all the other grains in the mixer before finally ending up in your ears.
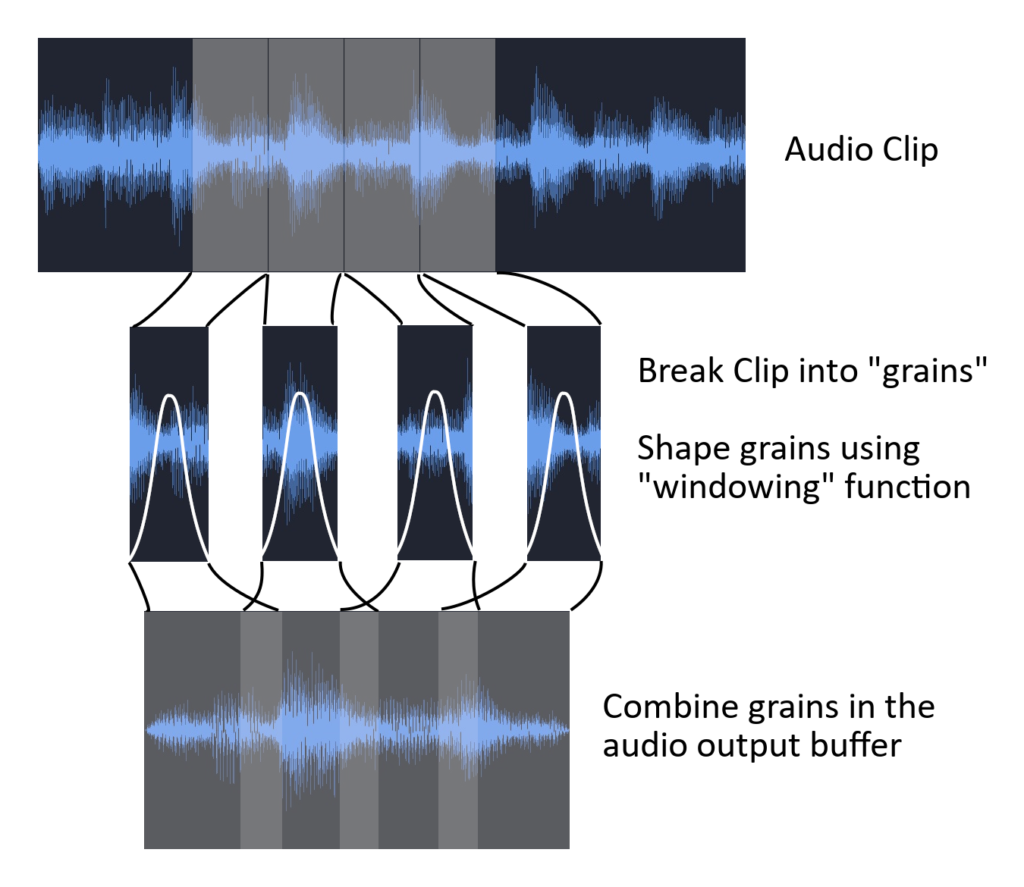
Basic Granular Synthesis model. By Chris Vik (CC0)
Garbage Collection and Pooling
Our takeaway: Instantiating grain objects as they’re needed and destroying them when they’re finished generates a ton of garbage collection. Use pooling prevent memory management from hogging the CPU.
One of the first issues we came up against was garbage collection. Grains have a very short lifespan. You create an object, let it play, then once the grain is finished you throw out the object, right? Unfortunately, this intuitive approach of creating and destroying grain objects as needed creates a massive amount of garbage collection for Unity3D to deal with. It causes large spikes in CPU load as C# tries desperately to free up the memory allocated to all the grains that have been emitted. Because we were emitting and destroying hundreds or even thousands of grains per second, garbage collection was immense. Fortunately, this is a relatively painless issue solved by pooling, which permanently holds on to the memory needed for the maximum number of grains.
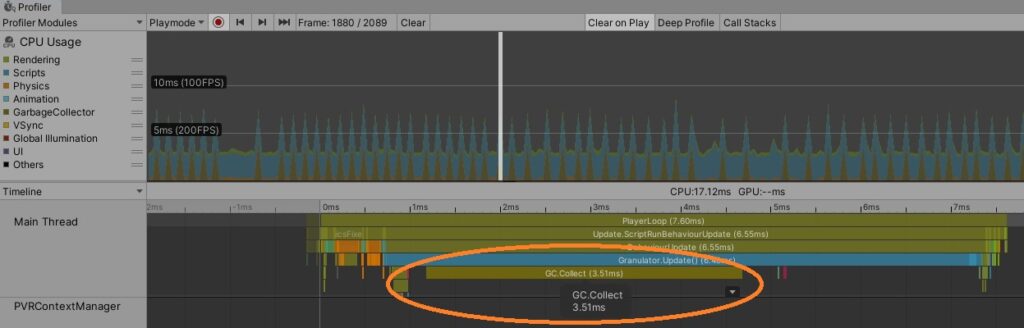
Too many spikes of garbage collection from assigning new GrainData objects for each grain, instead of recycling them using pooling.
Pooling permanently allocates the memory required to produce the maximum desired number of grains, each with a length limited to 1000 ms. This was done by creating two dynamic lists: active and inactive grains. On startup, the inactive pool is filled with grain objects. At each update call, the grain manager determines the number of grains to be played this update, picks grain objects from the inactive list, populates them with the necessary grain data, and moves them to the active list. This transfers the burden that would have been placed on the CPU over to the RAM. Since even a thousand grains contains less than 100MB of data, this was a an easy choice to free up a ton of CPU cycles for loads more stability grains.
DSP Timing
Our takeaway: Frame rates aren’t stable or fast enough to trigger audio in true real-time. Create a global DSP clock to manage grain timing and make the grain queue duration each frame slightly longer than the frame delta to avoid stutter or gaps when frames take longer than expected.
As far as audio engine buffer sizes, these numbers are horrible.
DSP Buffer
So that we separate grain trigger times from Unity3D’s update call, we created a DSP clock to keep a tally of the audio samples, which we can use to trigger grains between this frame and the next. However, this counter and the process of populating the audio output cannot be made on every single audio sample, but is instead called in chunks. This is the DSP buffer, accessible in C# through the OnAudioFilterRead call.
void OnAudioFilterRead(float[] data, int channels)
{
for (int dataIndex = 0; dataIndex < data.Length; dataIndex += channels)
{
_CurrentDSPSample++;
}
}The frequency of the OnAudioFilterRead call is a function of the sample rate (Project Settings > Audio > System Sample Rate), and buffer size (Project Settings > Audio > DSP Buffer Size) settings in Unity. The DSP Buffer Size determines how many audio samples are processed at each OnAudioFilterRead call, therefore, how often it’s called. If we assume a common sample rate of 44,100 Hz, and place a Debug.Log(data.Length) line inside OnAudioFilterRead, we can calculate how often the call is made:
- Best Latency = 512 samples / 44,100 x 1,000 (ms per second) = ~11.6 ms per call
- Good Latency = 1024 samples/ 44,100 x 1,000 (ms per second) = ~23.3 ms per call
- Best Performance = 2048 samples / 44,100 x 1,000 (ms per second) = ~46.4 ms per call
As far as audio engine buffer sizes, these numbers are horrible. Most digital audio workstations (DAWs) allow processing buffers with sizes of 64 samples (1.45 ms) or even less. But, this is a games engine, after all, so we have to play with the cards we’re dealt. The number can be improved by increasing the sample rate (such as 48,000 or 96,000), however this will increase CPU load and is bound to limitations of the user’s sound device. Since 44,100 is the most common, we’ll stick with this safe number. Likewise, a smaller buffer size reduces will reduce latency, but increases CPU load due to the increasing regularity of the DSP calls. So there is a balance to be made.
Grain Underrun and Audio Buffer Syncronisation
The frame update (or fixed update, it doesn’t matter) call is the only chance we have to process the environment, instantiate grains, populate them with data, and send them on their way. Since we want to create grains at intervals far smaller than how long a frame update happens, we need to create a grain queue each frame to make sure there are enough grains to populate the audio system until the next update. If the grain queue is shorter than the update call, we’ll run out of grains to play and end up with what we call grain underrun, causing clicks, pops, gaps and mistimed grains.
If the grain queue is shorter than the update call, we’ll run out of grains to play and end up with what we call grain underrun, causing clicks, pops, gaps and mistimed grains.
To solve this, we provide the grain queue with a duration value that’s slightly longer than the frame. How much longer? Since we don’t actually know how long the next update will take, we unfortunately need to do some guessing. The bottom line is that it needs to be set at a value that is always larger the longest possible time between frames.
As the queue duration increases, so too does latency between the interactions and sonic output, since new grains will only be added after the current queue is finished. When a grain queue overlaps into the next frame, the duration it overlaps for will be subtracted from the current frame’s total queue duration. For instance, if we set the queue duration to 100ms, we’ll always have grains to play (unless the FPS goes under 10, if it does we’ve got bigger problems), but no new grains can be played until the current queue is finished. In this case, the sonic output of the system will only change once every 7 or 8 frames of interaction. This has the potential create a very unresponsive audio/visual experience.
We could either hard-code some “reasonable” queue duration based on our target frame rate, or employ some smarts by using frame deltas (Time.deltaTime) plus a small amount of added duration that accounts for a worst-case frame delta change. We opted for the latter, since it decreases latency on well-performing systems, and generally avoids grain underrun by increasing latency when the system is under heavy load.
Below is an example of how we’ve managed the creation of sample accurate grains, despite the variable duration of each frame. The numbers shown are not what to necessarily expect from the system, but are accurately calculated to represent the ratio of efficiency between the methods.
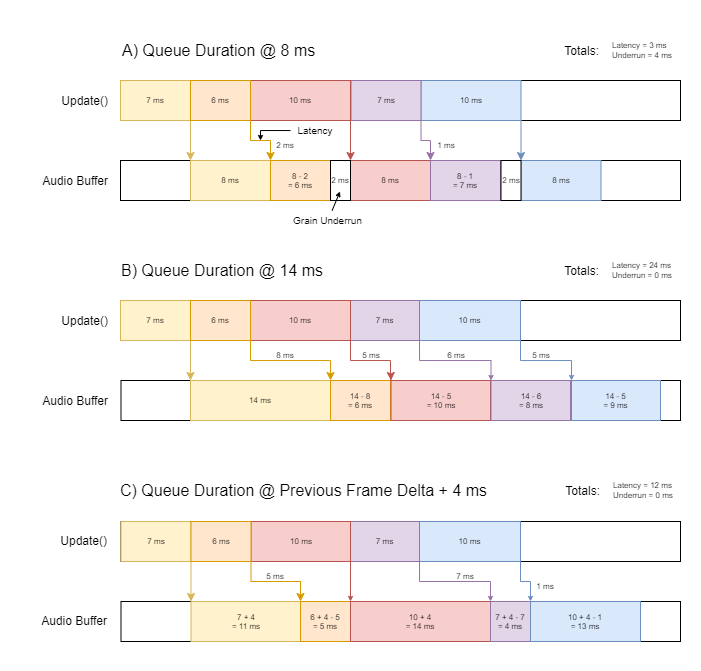
How we optimised the queue duration to avoid underrun while minimising latency by using previous frame delta. Each coloured box represents the duration of the Update call, and the grain queue fed to the audio buffer from that Update call. Note how the latency is subtracted from the queue duration.
You can see that hard-coding a queue duration that’s too low (A) results in grain underrun (identified as white spaces in the Audio Buffer), which is something we absolutely want to avoid. By hard-coding a duration that’s too high (B), we end up with an excessive amount of latency. A solution is to take the frame delta and add a tiny amount of hard-coded duration (C), which results in zero underrun and well optimised latency.
In the future, we may consider building a smarter system that actively lowers queue duration until a single instance of grain underrun is detected and adjusts accordingly. This is not dissimilar to how engine knock sensors adjust ignition timing in modern cars. But that’s enough optimisation for today.
A Short Note on Latency
One of the highest priories in digital music tools is keeping the lowest possible latency between the user’s interaction and the expected sonic result. This is especially important with discrete and percussive musical actions, such as drumming. Latency is necessary for any DSP implementation, but we need to be clear that the latency described above is added to the latency already existing in the entire system’s DSP chain, and therefore for it to be minimised.
Fortunately, this is slightly less important in continuous musical interactions and semi-generative systems, where the user is not directly involved in the triggering of a sharp sound. Granular synthesis is typically one such approach to music creation, so while adding 20 ms of latency to a drum machine might detract from the musician’s experience, this is might not even be noticeable in our environment.
With our frame and audio buffer all synced up and playing nicely, our next post will cover three approaches to integrate the granular synthesiser into the game world, taking processor load, spatialisation, and interactivity into account.